Guide to Variance Covariance Value at Risk Calculations
Variance and Covariance Matrix
To obtain the VarCov Matrix,
Step 1: Obtain change in prices we have exposure to for last 20 days.
Step 2: Obtain the covariance between the price changes of each price series.
The Covariance between 2 identical price series is the variance.
When we do this for all n x n price series, we obtain the variance covariance matrix.
Formulae for Covariance (below)
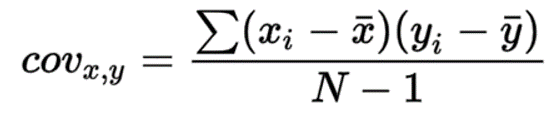
where:
Xi – the values of the price series X
Yj – the values of the price series Y
X̄ – the mean (average) of the price series X
Ȳ – the mean (average) of the price series Y
n – the number of data points
Weightage
Once we obtain the VarCov matrix, we need to find the weightage of each forward price series in our position.
Weightage is defined by our exposure for each forward price series divided by our total exposure.
Final Calculation
Lastly for calculations of VaR,
Total Portfolio 5%VaR
= 1 tailed z score at 95% confidence x Absolute value of Total Exposure Value x Variance of portfolio
= 1.645 x absolute value of (Total Exposure Value) x ( weight of a^2 x Variance of a + weight of b^2 x Variance of b + weight of c^2 x Variance of c + ...
+2 weight of a x weight of b x Covariance of a&b
+2 weight of a x weight of c x Covariance of a&c
+2 weight of b x weight of c x Covariance of b&c
+ …
)^0.5)
We use an absolute value since we may have net negative exposure.
Assumptions
• Changes in commodity prices are normally distributed.
• Variance and covariance obtained from the last 20 days is stable.
Browse More
- Overview
- Key terminology
- Understanding Item References
- Variance Covariance VaR calculations
